AGT: W2
2020-11-24 ( 2020-11-24)Dato da fare la scorsa volta:
Scrivere un notebook python/sagemath (dopo averlo correttamente installato?) che dato un grafo (assegnato come complesso simpliciale astratto) calcola i due gruppi di omologia \(H_0\) e \(H_1\). Opzionale: assegnare (in qualche modo razionale) delle coordinate ai vertici, trasformandolo in grafo possibilmente euclideo, e visualizzare quel che viene.
# define a function for visualization:
import matplotlib as mpl
import matplotlib.pyplot as plt
from matplotlib.collections import LineCollection
import numpy as np
mpl.rcParams['figure.figsize'] = (8.0, 8.0)
pi=np.pi
def view(X,show_labels=False):
vertices,edges=X # assign names...
fig=plt.figure()
ax=fig.gca()
ax.set_aspect('equal')
ax.set_axis_off()
fig.set_facecolor('white')
lc = LineCollection(edges, color="black", lw=2)
ax.add_collection(lc)
for P in vertices:
ax.add_patch(plt.Circle(P, 0.005*N/2, edgecolor='black',
linewidth=2, rasterized=False, antialiased=True,facecolor='w',
zorder=1000) )
if show_labels:
for j in range(len(vertices)):
Px,Py=vertices[j]
ax.annotate("$%s$" % j, vertices[j] , (Px-0.06,Py+0.01),fontsize=24, color='blue')
ax.plot() #Causes an autoscale update.
plt.show()# Primo problema: come **codificare** un grafo: elenco di vertici (euclidei?) e di spigoli.
N=3 #numero di case/pozzi
import random
A=[(random.random(),random.random()) for x in range(N)] # complesso simplicial astratto o euclideo
B=[ (random.random(), random.random()) for y in range(N)] # (niente cooordinate o coordinate?)
vertices = A + B # concatenation of lists (overloading degli operatori)
edges = [ [x, y] for x in A for y in B[1:] ] # math notation
# un grafo quindi è la coppia:
X = (vertices,edges) # come complesso simpliciale mancherebbero gli 0-simplessi, però...
# proviamo a scrivere una funzione per calcolare l'omologia: h_0 e h_1: prima
# di tutto dovremmo capire se è connesso oppure no...
view(X,show_labels=True)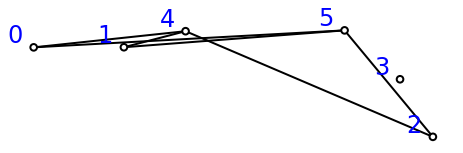
# now: come calcolare le componenti connesse? e l'omologia? come fare?
# Classico: https://en.wikipedia.org/wiki/Breadth-first_search
from scipy.sparse import csr_matrix
from scipy.sparse.csgraph import connected_components
# quindi: h_0 è il numero delle componenti connesse:
def h0(X):
vertices,edges = X
incidence_matrix = np.zeros((len(vertices),len(vertices)))
for s in edges:
x=vertices.index(s[0])
y=vertices.index(s[1])
incidence_matrix[x,y] = 1
incidence_matrix[y,x] = 1
graph = csr_matrix(incidence_matrix)
n_components = connected_components(csgraph=graph, directed=False, return_labels=False)
return n_components
print(h0(X))
2# ora calcoliamo h_1: teniamo conto che h_0 - h_1 = c_0 - c_1 :
# segue che h_1 = h0 - c_0 + c_1
def h1(X):
vertices, edges = X
c0 = len(vertices)
c1 = len(edges)
return h0(X) - c0 + c1
print(h1(X))2# e per dare delle coordinate migliori di quelle random?
import scipy.optimize
elastic_constant=1.0
def sq_euc_norm(P):
result=0.0
for j in range(len(P)):
result += P[j] * P[j]
return result
def euc_norm(P):
sq_result = sq_euc_norm(P)
return sq_result ** (0.5)
def distance(P, Q):
result = euc_norm(P-Q)
return result
def vector_product(P,Q):
vector_product=np.zeros(3)
vector_product[0] = P[1] * Q[2] - Q[1] * P[2]
vector_product[1] = Q[0] * P[2] - P[0] * Q[2]
vector_product[2] = P[0] * Q[1] - Q[0] * P[1]
return vector_product
def dot_product(P,Q):
return np.dot(P,Q)
def Uij(P,Q,are_endpoints=False):
"""interaction of P and Q: edges elastic attract, all repulsive"""
if are_endpoints:
return elastic_constant * sq_euc_norm(P-Q) + 1. / euc_norm(P-Q)
else:
return 1. / euc_norm(P-Q)
def grad_Uij(P,Q,are_endpoints=False):
"""grad of interaction of P and Q, wrt P"""
if are_endpoints:
return 2.0 * elastic_constant * (P-Q) - (P-Q) * euc_norm(P-Q)**(-3.)
else:
return - (P-Q) * euc_norm(P-Q)**(-3.)
def potential(conf,is_edge):
energy = 0.0
number_of_vertices,eucl_dim=conf.shape
# numba.prange requires parallel=True flag to compile.
# It causes the loop to run in parallel in multiple threads.
for i in range(number_of_vertices-1):
for j in range(i + 1, number_of_vertices ):
if is_edge[i,j]:
energy += Uij( conf[i,:],conf[j,:], are_endpoints=True )
else:
energy += Uij( conf[i,:],conf[j,:], are_endpoints=False)
return energy
def grad_potential(conf,is_edge):
number_of_vertices,eucl_dim=conf.shape
grad = np.zeros((number_of_vertices,eucl_dim))
for i in range(number_of_vertices-1):
for j in range(i + 1, number_of_vertices ):
if is_edge[i,j]:
grad[i,:] += grad_Uij( conf[i,:],conf[j,:], are_endpoints=True )
grad[j,:] += grad_Uij( conf[j,:],conf[i,:], are_endpoints=True )
else:
grad[i,:] += grad_Uij( conf[i,:],conf[j,:], are_endpoints=False )
grad[j,:] += grad_Uij( conf[j,:],conf[i,:], are_endpoints=False )
return grad
def euclidean_embedding(vertices,edges,dim=2):
number_of_vertices=len(vertices)
eucl_dim=dim
is_edge=np.zeros( (number_of_vertices,)*2 , dtype=bool)
for (i,j) in edges:
is_edge[i,j]=True
def opt_fun(x):
conf=x.reshape(number_of_vertices,eucl_dim)
result = potential(conf,is_edge)
return result
def opt_jac(x):
conf=x.reshape(number_of_vertices,eucl_dim)
result = grad_potential(conf,is_edge)
return result.reshape(number_of_vertices*eucl_dim)
X0=np.random.rand( number_of_vertices,eucl_dim )
result = scipy.optimize.minimize(opt_fun,X0,method='CG',jac=opt_jac)
outconf=result.x.reshape(number_of_vertices,eucl_dim)
howsol=euc_norm(result.jac)
print("howsol: {}".format(howsol))
# print(outconf)
eucl_vertices= [ tuple( outconf[i,:] ) for i in range(number_of_vertices) ]
eucl_edges= [ (eucl_vertices[i],eucl_vertices[j]) for i,j in edges ]
return (eucl_vertices,eucl_edges)
N=5 #numero di case/pozzi
A=[x for x in range(N)] # complesso simplicial astratto o euclideo
B=[ y for y in range(N,N+N)] # (niente cooordinate o coordinate?)
vertices = A + B # concatenation of lists (overloading degli operatori)
edges = [ [x, y] for x in A for y in B ] # math notation
print(vertices,edges)
eucl_S=euclidean_embedding(vertices,edges)
view(eucl_S,show_labels=True)[0, 1, 2, 3, 4, 5, 6, 7, 8, 9] [[0, 5], [0, 6], [0, 7], [0, 8], [0, 9], [1, 5], [1, 6], [1, 7], [1, 8], [1, 9], [2, 5], [2, 6], [2, 7], [2, 8], [2, 9], [3, 5], [3, 6], [3, 7], [3, 8], [3, 9], [4, 5], [4, 6], [4, 7], [4, 8], [4, 9]]
howsol: 1.4563980367849192e-05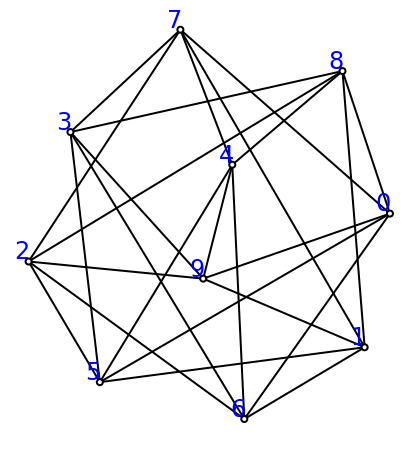
N=7
vertices = [ x for x in range(N)]
edges = [ sorted( [x, (x+1) % N] ) for x in range(N)] + \
[ sorted( [x,(x+3) %N ]) for x in range(N) ]
print(vertices,edges)
eucl_S=euclidean_embedding(vertices,edges)
view(eucl_S,show_labels=True)[0, 1, 2, 3, 4, 5, 6] [[0, 1], [1, 2], [2, 3], [3, 4], [4, 5], [5, 6], [0, 6], [0, 3], [1, 4], [2, 5], [3, 6], [0, 4], [1, 5], [2, 6]]
howsol: 3.9716886522722156e-06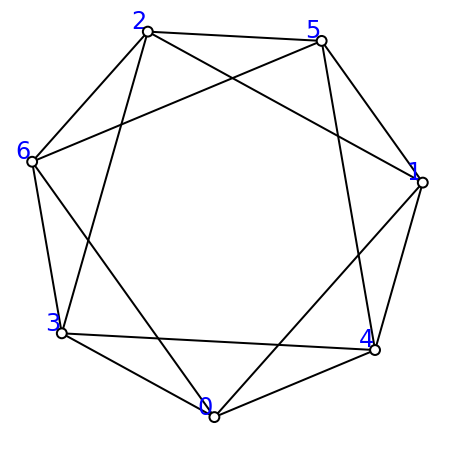
Quindi da fare…
Provare a fare eseguire i pezzi sopra di codice (copia-e-incolla), modificandoli qua e là. Quale potenziale è meglio per rappresentare visualmente i grafi? Qualcosa in 3d? E se ciascuno riuscisse a portare su e-learning l’immagine di un grafo di cui si è calcolato l’omologia? Fare piccola una galleria?