AGT: W1

Installare CAS, python, jupyter, sagemath?

Per poter fare un po’ di matematica computazionale serve avere un calcolatore e degli strumenti di calcolo. Potrebbe bastare un abaco, una copia del Liber Abbaci di Fibonacci per imparare ad usare le cifre decimali (PDF oppure SpringerLink), un regolo calcolatore oppure qualcosa di più recente.

Una lista (molto incompleta) di strumenti di calcolo utili per la matematica:

• maple
• Mathematica
• matlab (with a toolbox)
• sagemath
• per python: SymPy, SciLab, SciPy, e molti altri…
• jupyter

Quali installare, e come?

Io consiglio, prima di iniziare, di preparare un ibrido di linux e Windows: il Windows Subsystem for Linux. Le istruzioni per l’installazione non sono troppo complicate da seguire, almeno per una distribuzione standard come la ubuntu. Poi nella parte linux si possono installare sagemath e jupyter con il gestore di pacchetti. In un certo senso, linux e Mac OS X sono già ibridi di linux e windows.

 $ sudo apt install jupyter-notebook 
 $ sudo apt install sagemath sagemath-jupyter

Oppure, c’è il progetto Anaconda.

Per chi proprio non ha tempo, e vuole provare senza installare niente, c’è l’ottimo Google Colab, che dà accesso ad un notebook jupyter senza dover configurare o installare alcunché.

Ma cos’è un notebook? È come questo documento (che state leggendo): un alternarsi di blocchi di testo formattato (text cells) e di blocchi di codice python/sagemath (code cells) con l’output dei blocchi di codice.

Vediamo un esempio.

n=4
print(factorial(n))
# ora proviamo una sequenza di comandi più complessa.
x,y=var('x,y') # qua sto scrivendo un commento. sympy
import matplotlib as mpl # importare una librerie
mpl.rcParams['figure.figsize'] = (8.0, 8.0) # per avere figure più grandi
p=streamline_plot((cos(x),sin(y)),(x,-4,4),(y,-4,4) ,aspect_ratio=1) 
p.show()

24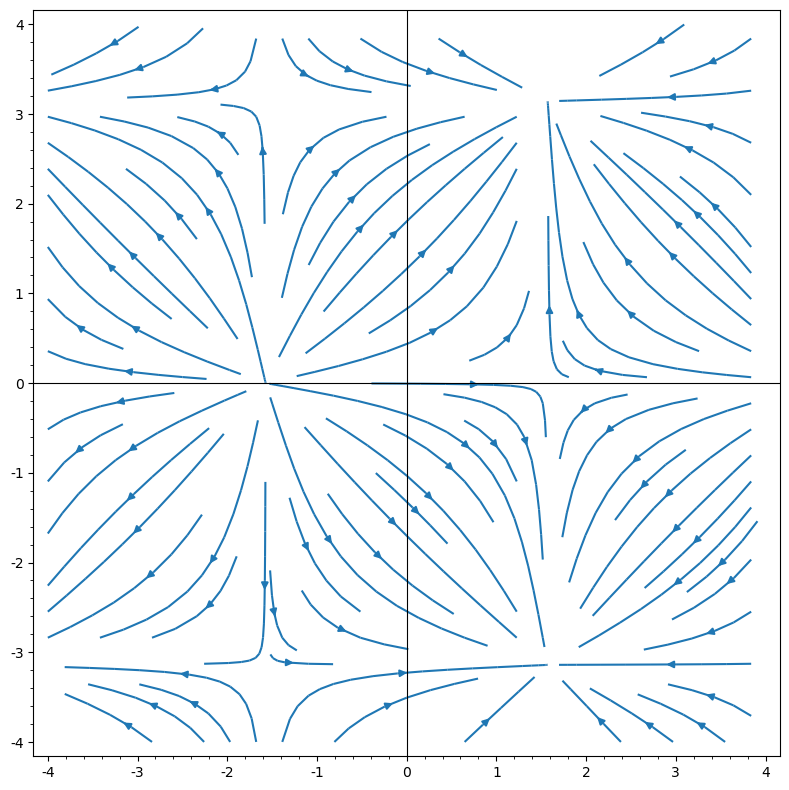

Come si capisce in questo esempio, l’output può essere un numero, un grafico, una struttura astratta, un testo, qualsiasi cosa.

L’unica cosa da ricordare è che per poter eseguire i blocchi di codice in un jupyter notebook occorre premere la combinazione di tasti SHIFT+ENTER quando il cursore è nel blocco. A questo punto potete seguire gli ottimi tutorial preparatori:

• Crash into Python: Python for Programmers with 3 Hours
• Jupyter: Get Started
• Introductory Sage Tutorial
• A Primer on Scientific Programming with Python (SpringerLink Book PDF, sfortunatamente python2/obsoleto)

Altri progetti per condividere calcoli e lavorare con notebook condivisi: - Azure Notebooks - CoCalc - Binder - Kaggle Kernels - OpenDreamKit

Visualizzare (complessi simpliciali e strutture)

Una delle funzionalità più interessanti dei calcolatori, oltre al calcolare, è quello che aiutano a visualizzare gli oggetti (grafici di funzioni, sistemi dinamici, oggetti in 2D o 3D, …).

Prendiamo quindi un grafo euclideo, cioè una coppia data da un insieme di vertici che sono punti di \(\mathbb{R}^d\) con \(d=2,3\), e di spigoli. \[ K = (X_K,\Phi_K) \] Per esempio, il grado completo bipartito \(K_{3,3}\) (chiamato anche utility graph). Ha sei vertici \[ A_1=(0,0),~ A_2=(0,1),~ A_3=(0,2),~ B_1=(1,0),~ B_2=(1,1),~ B_3=(1,2), \] e gli spigoli che collegano ogni \(A_i\) con ogni \(B_j\), cioè \[ \begin{aligned} X_K & = \{ A_1,A_2,A_3, B_1, B_2, B_3 \}, \\ \Phi_K & = \{ A_1, A_2, A_3, B_1, B_2, B_3, A_1B_1, A_1B_2, A_1B_3, A_2B_1, A_2B_2, A_2B_3, A_3B_1, A_3B_2, A_3B_3 \} \end{aligned} \] dove omettiamo le (inutili) parentesi per rappresentare i simplessi.

Proviamo a costruire un prototipo di grafo in python e a visualizzarlo con matplotlib.

N=3 #numero di case/pozzi
A=[(0,j) for j in range(N)] # [ (0,j) per j = 1 .. N (python: 0..N-1)]
B=[(N/2,j) for j in range(N)]
vertices = A + B # concatenation of lists (overloading degli operatori)
edges = [ [x, y] for x in A for y in B ] # math notation

import matplotlib.pyplot as plt
from matplotlib.collections import LineCollection


fig=plt.figure()
ax=fig.gca()
ax.set_aspect('equal')
ax.set_axis_off()
fig.set_facecolor('white') # dettagli del second'ordine

lc = LineCollection(edges, color="black", lw=2)

ax.add_collection(lc)
for P in vertices:
    ax.add_patch(plt.Circle(P, 0.005*N/2, edgecolor='black',
                        linewidth=2, rasterized=False, antialiased=True,facecolor='w',
                        zorder=1000) )
for i in range(N):
    pA=vertices[i]
    pB=vertices[N+i]
    ax.annotate("$A_{%s}$" % (i+1),pA, (pA[0]-0.06*N,pA[1]+0.01),fontsize=24)
    ax.annotate("$B_{%s}$" % (i+1),pB, (pB[0]+0.01*N,pB[1]+0.01),fontsize=24)


ax.plot()   #Causes an autoscale update.
plt.show()

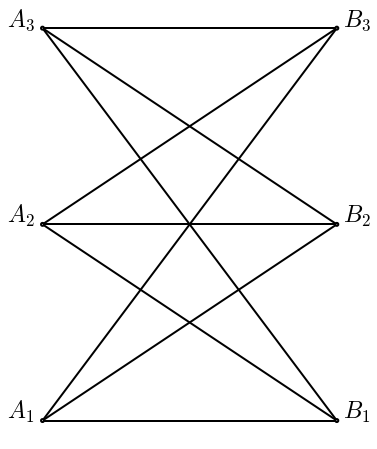
## proviamo con delle altre coordinate:
import matplotlib.pyplot as plt
from matplotlib.collections import LineCollection
import numpy as np
pi=np.pi

N=8
A=[(np.cos( 2*pi * (2*j) / float(2*N)) , 
     np.sin(2*pi*(2*j)/ float(2*N))) \
   for j in range(N)]
B=[(np.cos(2*pi*(2*j+1)/float(2*N)), 
    np.sin(2*pi*(2*j+1)/float(2 *N))) \
   for j in range(N)]
vertices = A + B # concatenation of lists
edges = [ [x, y] for x in A for y in B ] # math notation

fig=plt.figure()
ax=fig.gca()
ax.set_aspect('equal')
ax.set_axis_off()
fig.set_facecolor('white')

lc = LineCollection(edges, color="black", lw=2)

ax.add_collection(lc)
for P in vertices:
    ax.add_patch(plt.Circle(P, 0.005*N/2, edgecolor='black',
                        linewidth=2, rasterized=False, antialiased=True,facecolor='w',
                        zorder=1000) )
for i in range(N):
    pA=vertices[i]
    pB=vertices[N+i]
    ax.annotate("$A_{%s}$" % (i+1),pA, (pA[0]-0.03*N,pA[1]+0.01),fontsize=24)
    ax.annotate("$B_{%s}$" % (i+1),pB, (pB[0]+0.01*N,pB[1]+0.01),fontsize=24)


ax.plot()   #Causes an autoscale update.
plt.show()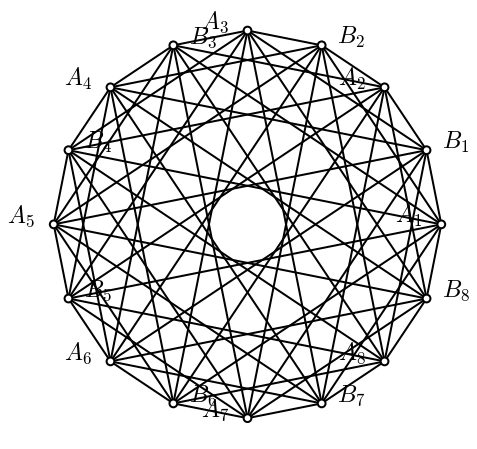

Forse è un po’ troppo laborioso… Proviamo a cercare pacchetti preconfezionati per visualizzare grafi e complessi simpliciali…

Grafi e complessi simpliciali astratti ed euclidei

In sagemath ci sono sia la parte per i grafi, che per i complessi simpliciali, come parte della sezione sui cell complexes and homology. Quanto sarà affidabile e comprensibile? Non c’è molto per la visualizzazione, ma c’è molto per il calcolo dell’omologia e per le generalizzazioni algebriche e combinatoriche.

Per i grafi, in realtà dietro sagemath c’è il python package networkx, con strumenti per la creazione, gestione e visualizzazione di grafi. Quando vale la pena spendere del tempo per installare e imparare ad usare un package? Difficile a dirsi… Purtroppo bisogna provare, e fidarsi un po’ del peer review.

T = simplicial_complexes.Torus()
help(T)

Help on UniqueSimplicialComplex_with_category in module sage.homology.examples:

Minimal triangulation of the torus

stnc = 'argomenti di geometria e topologia'
g = DiGraph({}, loops=False, multiedges=True)
for a,b in [(stnc[i], stnc[i + 1]) for i in range(len(stnc) - 1)]:
    g.add_edge(a, b,b)
g.plot(color_by_label=True, edge_style='solid').show(figsize=(8,8))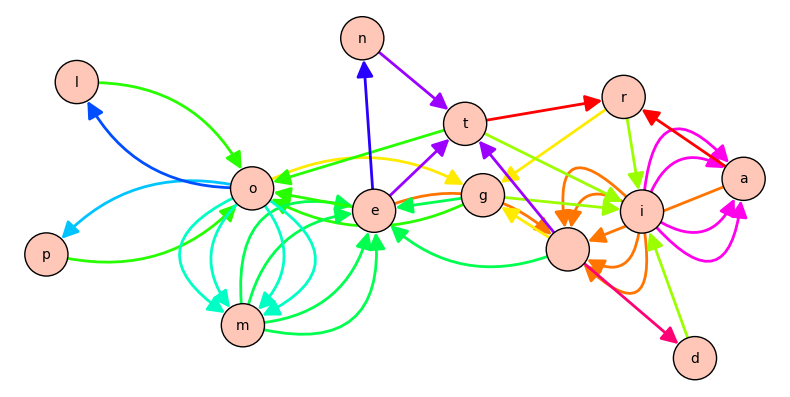

La documentazione non è chiarissima; e purtroppo il (bellissimo) grafo diretto viene rappresentato con delle frecce in più. Ci sarà qualche bug da qualche parte in sagemath? Dove? Altro problema: per i complessi simpliciali non sembra esserci qualcosa per visualizzarli… Proviamo di nuovo con il Toro:

print("Vertici:", T.vertices())
print("Simplessi:", T.faces())

Vertici: (0, 1, 2, 3, 4, 5, 6)
Simplessi: {-1: {()}, 0: {(2,), (3,), (1,), (6,), (5,), (4,), (0,)}, 1: {(1, 4), (4, 6), (2, 3), (2, 6), (4, 5), (0, 1), (3, 6), (0, 5), (1, 5), (3, 4), (0, 6), (1, 2), (0, 3), (0, 2), (2, 5), (0, 4), (2, 4), (5, 6), (3, 5), (1, 6), (1, 3)}, 2: {(0, 3, 4), (0, 4, 6), (1, 2, 4), (1, 3, 6), (0, 1, 2), (0, 2, 6), (2, 4, 5), (2, 3, 6), (2, 3, 5), (0, 1, 5), (0, 3, 5), (4, 5, 6), (1, 3, 4), (1, 5, 6)}}

Osserviamo che è un complesso simpliciale astratto, con 7 vertici. Quanti sono i simplessi di dimensione 1 e 2? Perché dovrebbe essere un toro? Cosa significa “triangolazione minimale del toro”? Un toro ha Caratteristica di Eulero-Poincaré uguale a \(0\), quindi \[ c_0 - c_1 + c_2 = 0 \] dove \(c_j\) rappresenta il numero di simplessi di dimensione \(j\). In altre variabili \[ v - s + f = 0. \] Visto che è una superficie, ogni \(1\)-simplesso appartiene esattamente a \(2\) \(2\)-simplessi: quindi \(3f = 2s\): \[ 0 = v - s + f = v - s + \frac{2}{3} s \implies s = 3v. \] In totale, poi, non ci possono essere più di \(\binom{v}{2}\) \(1\)-simplessi: dunque \[ 3v = s \leq \dfrac{v(v-1)}{2} \implies 6 \leq v-1 \implies v\geq 7. \] Quindi, in effetti, ogni triangolazione del toro deve avere almeno 7 vertici. Quella minimale, se ha 7 vertici allora ha 21 spigoli e quindi 14 facce.

Approfondimento: Toro di Császár

len( T.faces()[1]), len(T.faces()[2])

(21, 14)

Da fare:

Scrivere un notebook python/sagemath (dopo averlo correttamente installato?) che dato un grafo (assegnato come complesso simpliciale astratto) calcola i due gruppi di omologia \(H_0\) e \(H_1\). Opzionale: assegnare (in qualche modo razionale) delle coordinate ai vertici, trasformandolo in grafo possibilmente euclideo, e visualizzare quel che viene.